Niimi, R.; Furusawa, C.; Himeoka, Y.

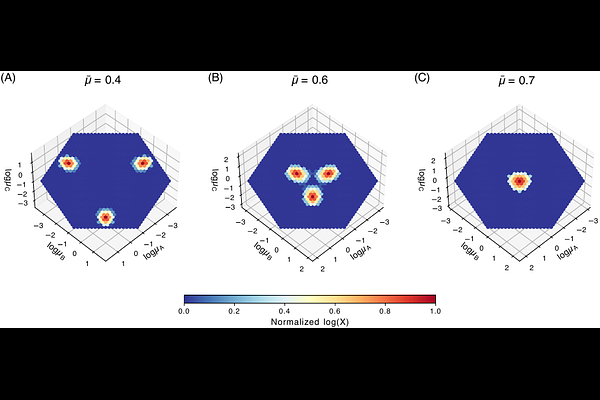
Microbial populations exhibit a broad spectrum of nutrient utilization strategies, ranging from strategies utilizing diverse nutrients, called \"generalist,\" to ones being highly adapted to specific nutrients, called \"specialists.\" The mathematical conditions for the diversification of nutrient utilization strategies are central questions in theoretical ecology. Previous studies have shown that trade-offs among different resource utilization functions that cells cannot utilize broad types of substrates at near-maximum speed are crucial for the emergence of diverse strategies. However, in natural settings, nutrient availability often fluctuates over time, imposing additional trade-offs on cells. Cells that grow rapidly under nutrient-rich conditions will suffer a higher death rate under nutrient-poor conditions, creating a growth-death trade-off that intersects with the classical resource-use trade-off. Here, we introduce a unified mathematical model that simultaneously incorporates the resource-use trade-off and the growth-death trade-off. The nutrient supply was modeled as discrete stochastic events, capturing realistic temporal fluctuations. We show that the relative balance between growth and death rates critically influences the dominance of either generalist or specialist strategies. Specifically, under conditions of high average growth rates among different environments and a weak trade-off between growth and death rates, generalists prevail. In contrast, when the growth-death trade-off is intense, specialists emerge as the dominant strategy. Our findings reveal that accounting for the growth-death trade-off is crucial for understanding how microbial communities adapt and evolve in temporally varying environments.