Sifan Wang, Zehao Dou, Tong-Rui Liu, Lu Lu

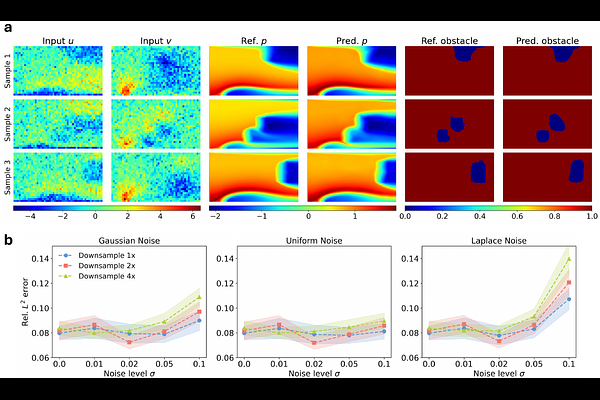
Recent advances in generative modeling -- particularly diffusion models and flow matching -- have achieved remarkable success in synthesizing discrete data such as images and videos. However, adapting these models to physical applications remains challenging, as the quantities of interest are continuous functions governed by complex physical laws. Here, we introduce $\textbf{FunDiff}$, a novel framework for generative modeling in function spaces. FunDiff combines a latent diffusion process with a function autoencoder architecture to handle input functions with varying discretizations, generate continuous functions evaluable at arbitrary locations, and seamlessly incorporate physical priors. These priors are enforced through architectural constraints or physics-informed loss functions, ensuring that generated samples satisfy fundamental physical laws. We theoretically establish minimax optimality guarantees for density estimation in function spaces, showing that diffusion-based estimators achieve optimal convergence rates under suitable regularity conditions. We demonstrate the practical effectiveness of FunDiff across diverse applications in fluid dynamics and solid mechanics. Empirical results show that our method generates physically consistent samples with high fidelity to the target distribution and exhibits robustness to noisy and low-resolution data. Code and datasets are publicly available at https://github.com/sifanexisted/fundiff.