Z. Cao, P. G. Jonker, S. Wen, N. C. Stone, A. I. Zabludoff

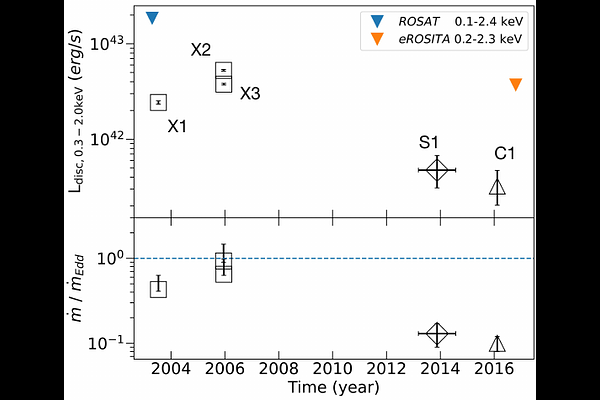
We fit the evolving X-ray spectra of the variable and fading source 2XMM J123103.2+110648 (J1231), which is an intermediate-mass black hole (IMBH) candidate. Recent X-ray timing studies have proposed that J1231's quasi-periodic oscillation (QPO) observed at the peak of its X-ray lightcurve is a variant of the quasi-periodic eruptions (QPEs) observed in other sources. Here, we fit X-ray spectra from XMM-Newton, Swift, and Chandra using a slim disc model for the black hole's accretion disc, obtaining a best-fit black hole mass of ($6\pm3)\times10^{4}$ $M_\odot$ and spin of $>0.6$ at 2$\sigma$ confidence. This mass is consistent with past estimates, supporting the IMBH interpretation, and the spin measurement is new. Yet the nature of J1231 remains uncertain: its long-term variability (decade-long continuum evolution) could signal a tidal disruption event or active galactic nuclear variability. We find that the spectral evolution within the first three years after the source's detection can be well explained by either a varying disc accretion rate $\dot m$ or a varying disc inclination $\theta$. Meanwhile, we find that during the short-term variability (the QPO with a ~3.8hr period), each oscillation does not show the "hard-rise-soft-decay" typical of QPEs. We fit the average spectrum at the QPO lightcurve maxima and the average spectrum at its minima, finding that the spectral difference is well explained by $\dot m$ decreasing from peaks to valleys if $\theta<30^{\circ}$ and constant between all data epochs. This result suggests that the short-term QPO behaviour might also be driven by a varying disc $\dot m$.