A Game-Theoretic Quantum Algorithm for Solving Magic Squares
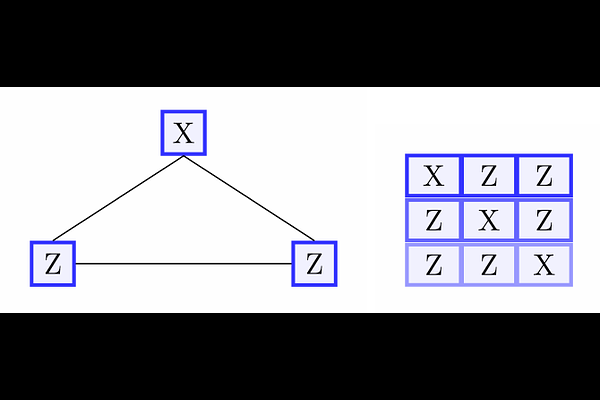
A Game-Theoretic Quantum Algorithm for Solving Magic Squares
Sarah Chehade, Andrea Delgado, Elaine Wong
AbstractVariational quantum algorithms (VQAs) offer a promising near-term approach to finding optimal quantum strategies for playing non-local games. These games test quantum correlations beyond classical limits and enable entanglement verification. In this work, we present a variational framework for the Magic Square Game (MSG), a two-player non-local game with perfect quantum advantage. We construct a value Hamiltonian that encodes the game's parity and consistency constraints, then optimize parameterized quantum circuits to minimize this cost. Our approach builds on the stabilizer formalism, leverages commutation structure for circuit design, and is hardware-efficient. Compared to existing work, our contribution emphasizes algebraic structure and interpretability. We validate our method through numerical experiments and outline generalizations to larger games.