Maga Grafe, Kaixuan Zhou, Zaman Tekin, Zhiyuan Lin, Sen Li, Fengquan Zhang, Valentin Ivannikov, Tim Byrnes

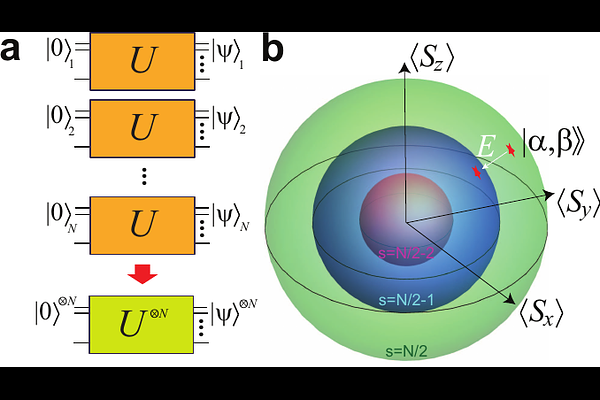
We introduce a novel type of quantum error correcting code, called the spinor code, based on spaces defined by total spin. The code is a nonstabilizer code, and is also a nonlinear quantum error correcting code, meaning that quantum information is encoded in a parameterized family of quantum states, rather than a linear superposition of code words. Syndrome measurements are performed by projecting on states with differing total spin, with an associated correction to map states back to the maximum total spin space. We show that the code is asymptotically capable of protecting against any single qubit Pauli error for Gaussian distributed states such as spin coherent state. We directly evaluate the performance under the depolarizing channel, considering various cases, with and without initialization and measurement errors, as well as two qubit errors. We estimate the code-capacity threshold to be in the range of 32-75%, while the phenomenological threshold is in the range 9-75%.