Jiaqi Leng, Bin Shi

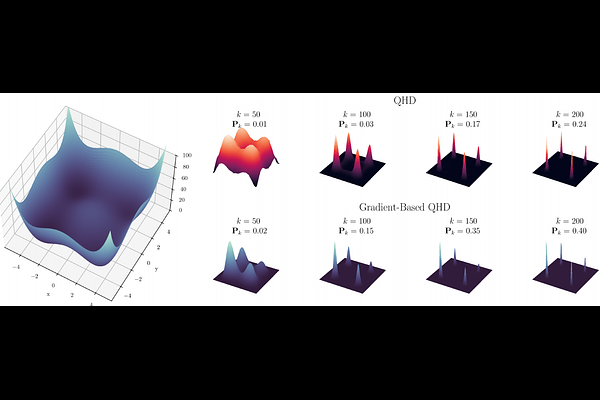
With rapid advancements in machine learning, first-order algorithms have emerged as the backbone of modern optimization techniques, owing to their computational efficiency and low memory requirements. Recently, the connection between accelerated gradient methods and damped heavy-ball motion, particularly within the framework of Hamiltonian dynamics, has inspired the development of innovative quantum algorithms for continuous optimization. One such algorithm, Quantum Hamiltonian Descent (QHD), leverages quantum tunneling to escape saddle points and local minima, facilitating the discovery of global solutions in complex optimization landscapes. However, QHD faces several challenges, including slower convergence rates compared to classical gradient methods and limited robustness in highly non-convex problems due to the non-local nature of quantum states. Furthermore, the original QHD formulation primarily relies on function value information, which limits its effectiveness. Inspired by insights from high-resolution differential equations that have elucidated the acceleration mechanisms in classical methods, we propose an enhancement to QHD by incorporating gradient information, leading to what we call gradient-based QHD. Gradient-based QHD achieves faster convergence and significantly increases the likelihood of identifying global solutions. Numerical simulations on challenging problem instances demonstrate that gradient-based QHD outperforms existing quantum and classical methods by at least an order of magnitude.