Roy, A.; Satten, G.; Zhao, N.

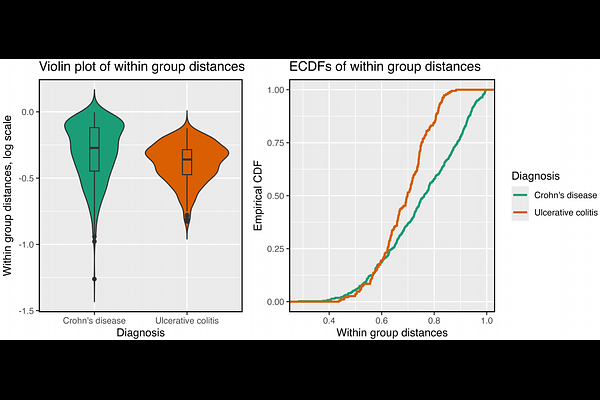
Testing homogeneity across groups in multivariate data is an important scientific question in its own right, as well as well as an auxiliary step in verifying the assumptions of ANOVA. Existing methods either construct test statistics based on the distance of each observation from the group center, or as the mean of pairwise dissimilarities among observations in a group. Both approaches can fail when mean within-group distance is similar across groups but the distribution of the within-group distances are different. This is a pertinent question in high dimensional microbiome data, where outliers and overdispersion can distort the performance of a mean-dissimilarity-based test. We introduce the non-parametric Distance based Test for Homogeneity (DTH) which measures dissimilarity between groups by comparing the empirical distribution of within-group dissimilarities using a combination of the Kolmogorov-Smirnov and Wasserstein distances. For more than two groups, pairwise group tests are combined using a permutation-based p-value. Through simulations we show that our method has higher power than existing tests for homogeneity in certain situations and comparable power in other situations. We also provide a simple framework for extending the test to a continuous covariate.