Rishi Goel, Casey R. Myers, Sally Shrapnel

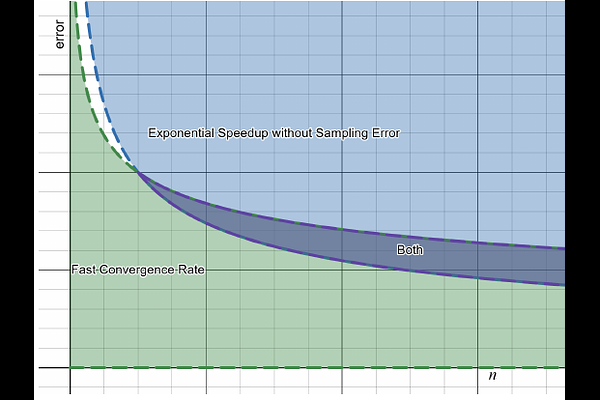
Modern machine learning methods typically fail to adequately capture causal information. Consequently, such models do not handle data distributional shifts, are vulnerable to adversarial examples, and often learn spurious correlations. Causal machine learning, or causal inference, aims to solve these issues by estimating the expected outcome of counterfactual events, using observational and/or interventional data, where causal relationships are typically depicted as directed acyclic graphs. It is an open question as to whether these causal algorithms provide opportunities for quantum enhancement. In this paper we consider a recently developed family of non-parametric, continuous causal estimators and derive quantum algorithms for these tasks. Kernel evaluation and large matrix inversion are critical sub-routines of these classical algorithms, which makes them particularly amenable to a quantum treatment. Unlike other quantum machine learning algorithms, closed form solutions for the estimators exist, negating the need for gradient evaluation and variational learning. We describe several new hybrid quantum-classical algorithms and show that uniform consistency of the estimators is retained. Furthermore, if one is satisfied with a quantum state output that is proportional to the true causal estimand, then these algorithms inherit the exponential complexity advantages given by quantum linear system solvers.