Victoria Laidlaw

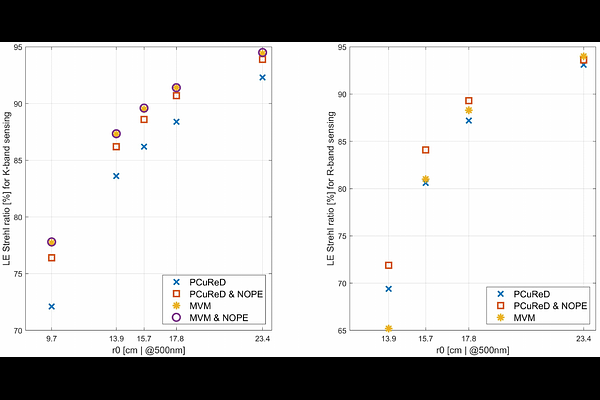
State-of-the-art adaptive optics (AO) systems perform non-linear Fourier-type wavefront sensing for real-time corrections of dynamic wavefront aberrations. This general class of sensors uses a filtering mask in the focal plane that converts phase fluctuations of the incoming light into intensity variations in the subsequent pupil plane. Due to their high sensitivity, Fourier-type wavefront sensors (WFSs) are the sensors of choice for many current and upcoming AO systems in ophthalmic imaging, free-space optical communications (FSOC) and astronomical ground-based telescopes such as the forthcoming generation of extremely large telescopes (ELTs). Conventionally, linear methods, like a matrix-vector-multiplication (MVM), are used for the inversion of Fourier-type WFSs. However, their non-linear behavior gives rise to severe performance degradations when significant channel perturbations are observed. They are expected to occur during strong atmospheric turbulence conditions, which are commonplace for non-rural sites and daytime observations. This study presents a novel type of iterative reconstructor to overcome non-linear wavefront sensing regimes. The underlying method is the non-linear Landweber iteration with Nesterov acceleration, well known in the field of inverse problems. A significant advantage of the new approach is its direct applicability to any Fourier-type WFS. This is implemented by adapting the filtering mask of the specific Fourier-type WFSs in the model-based algorithm. Several Fourier-type wavefront sensors are considered for ELT-scale instruments and their performance with the new algorithm is compared. The study goes on to concentrate on the pyramid wavefront sensor (PWFS), one of the most well-known Fourier-type WFSs. We demonstrate in end-to-end simulations that this novel approach outperforms linear methods in non-linear sensing regimes.